The model serves to understand the phenomena of chaos, when small deviations in the initial data lead to unpredictable consequences.

Meteorologist Edward Norton Lorenz found that the hydrodynamic equations he came up with to describe air transport in the atmosphere are very sensitive to the initial data. Thus, the famous phrase appeared that the flapping of the wings of a butterfly in Brazil can cause a tornado in Texas. Lorentz investigated the following equations, where x, y, z are related to the speed, density and temperature of the flows.

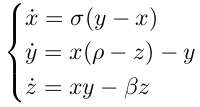
An attractor is a typical picture in the space of variables of a system of equations, when the system tends to equilibrium by a spiral or rotates around focal point. The Lorentz system of equations demonstrated a very atypical attractor with chaotic switching between two focal points, so this attractor was called the "strange Lorentz attractor". This example has become a classic demonstration that physical systems can be completely deterministic and yet unpredictable in nature even in the absence of quantum effects.

Examine how sensitive the solution is to perturbing the initial data. The delta parameter sets the deviations for the initial data of the second trajectory, which is drawn in green. The transition from one focus of an attractor to another physically means a strong change in the weather, which means that even with the most accurate model for calculations small errors in observation of initial conditions lead to the impossibility of accurately predicting the weather for a long time.